Sep 10, 2020 By Team YoungWonks *
What is an algorithm? Even as the transition to the digital world has been accelerated by the lockdown caused in turn by the outbreak of the Coronavirus, it is not surprising to see greater computer and smartphone penetration across the world. Which brings us to the relevant question: what makes these devices smarter than us humans? In a broad sense, the answer is rather simple: computers can computer (solve) many more problems than us, including more complex ones and that too at a faster rate. These problems could be calculations, data processing, automated reasoning, and other tasks. The computing power needed to perform these tasks in turn is fueled by what is called an algorithm.
In simpler terms, an algorithm is a procedure or formula for solving a problem, based on carrying out a sequence of specified actions. So a computer program is essentially an elaborate algorithm. In mathematics and computer science, an algorithm typically refers to a procedure that solves a recurring problem.
In this blog, we shall take a look at what is an algorithm, its evolution, its role in math and computers, and how they are expressed with the help of examples.
What is an algorithm?
The word algorithm comes from the 9th-century mathematician Muḥammad ibn Mūsā al-Khwārizmī, latinized as Algoritmi. As a widely read mathematician in Europe in the late Middle Ages - he was also known for his book on algebra - his name Al-Khwarizmi came to be known as algorismus in late medieval Latin, which then became algorism in English, and referred to the decimal number system. It was only in the late 19th century that the world algorithm caught on and came to mean what it does today in modern English.
As mentioned earlier, an algorithm refers to a procedure for solving a problem; this procedure typically plays out in a finite number of steps, and they frequently involve repetition of an operation. Interestingly, algorithms are not just used in mathematics and computer science but are also used in daily life. So, an informal definition of algorithm would describe it as a set of rules that precisely defines a sequence of operations. These rules could refer to computer programs (including programs that do not perform numeric calculations), a prescribed bureaucratic procedure or even a cook-book recipe. Typically, a program is an algorithm only if it stops eventually.
Let us look at a few examples of algorithms in our daily lives. Take for instance, the task of making tea. Now the algorithm here would be the set of instructions one would follow so as to make this tea. So, the algorithm would include the following steps:
- Heat water in a pan.
- Add to it - even as the water is warming up - crushed ginger.
- Add tea leaves.
- Add milk.
- When it comes to boil, add sugar.
- Let it simmer for 2 to 3 minutes.
Following the above instructions would produce the desired result and solve our problem/ fulfil the task.
Similarly, let's look at another example. Say, we wish to grow curry leaves in a pot. Now this is a task that can be carried out in different ways. This means there are multiple algorithms for this problem.
One algorithm would be about planting curry leaf seeds in a pot. So, this algorithm would read something like this:
- Take some soil in a pot.
- Sow fresh curry leaf seeds in this soil.
- Keep the seeds/ soil damp but not wet.
- Make sure the temperature is fairly warm (at least 20 degrees Celsius).
- Once it has taken root in a few weeks with enough warmth and moisture, make sure it continues to be in a well-drained pot and receives sunlight.
- Feed it weekly with fertilizer solution and trim the leaves as needed.
Another way of doing this (so, another algorithm in effect) would be about using fresh curry leaves with their stem. The steps here would be something like this:
- Treat the leaves as a cutting and insert into a soilless potting medium.
- Take a piece of stem from the tree that is fairly long and has several leaves.
- Remove the bottom 1 inch of leaves and immerse the bare stem into the medium.
- Water it thoroughly.
- Once it has taken root in around three weeks with enough warmth and moisture, plant the tree in a well-drained pot with good potting mix and keep it in a sunny area.
- Feed it weekly with fertilizer solution and trim the leaves as needed.
Algorithms in Mathematics and Computer Science
The definition of algorithm in a formal context, however, alludes to its role in the way data is processed. In computer systems, an algorithm is an instance of logic written in software-by-software developers and meant for the intended computer(s) to produce output from the given (sometimes zero) input.
So to get a computer to do a task, we need to write a computer program. Doing so means telling the computer, step by step, exactly what we want it to do. The computer then runs/ reads the program and executes the commands shared in it by following each step mechanically so as to complete the said task. This series of related commands or steps is a computer algorithm.
It is important to note that algorithms are a finite sequence of well-defined, computer-implementable problem-solving instructions and that thus there is no room for ambiguity. Starting from an initial state and sometimes initial input, the algorithm spells out instructions that cover a finite number of well-defined successive states, eventually yielding output and terminating at a final ending state.
Now let us turn to a few examples of algorithms in basic math.
Take for instance, a problem where one has to figure out if a given number (say 7) is odd or even.
Here the algorithm would comprise the following steps:
- Divide the number by 2. So here we divide 7 by 2.
- Check for the remainder. If the remainder is 0, the number is even and if the remainder is not zero, the number is odd. Here the remainder would be 1. Hence the number 7 is an odd number.
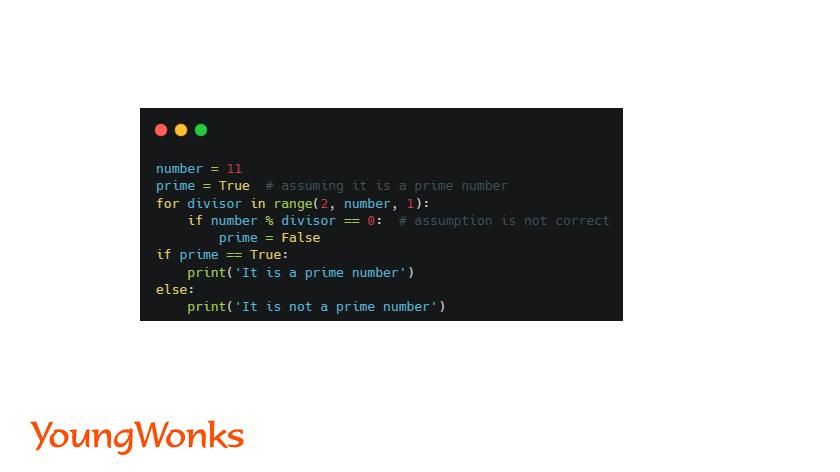
Similarly, let us look at yet another example. Say the problem here is figuring out if the number 11 is a prime number. Now a prime number is one that is divisible only by 1 and itself.
So here the algorithm for this problem would have these steps.
- Divide the number 11 by all numbers between 2 to 10 (since all numbers are divisible by 1 and themselves).
- So first divide 11 by 2 and check for the remainder.
- Then divide 11 by 3 and again check for remainder.
- Continue to divide 11 by other numbers 4, 5 and so on till you divide 11 by the number 10. Check for the reminder after each division.
- If the remainder after any of these divisions is 0, the number is not a prime number. If none of the remainders are 0, the number is a prime number. In this case, none of the remainders are zero. Hence, 11 is a prime number.
Types of algorithms
Just as in real life, in computer science and math as well, there are many types of algorithms available. In other words, often there are many ways - with different steps - of solving a given problem. All of these algorithms of course, need input to deliver a meaningful output.
Broadly speaking, algorithms, distinguished by their key features and functionalities, can be classified into six categories. Let's look at them here.
Greedy algorithm
A greedy algorithm is a type of algorithm that is typically used for solving optimization problems. So whenever one wishes to extract the maximum in minimum time or with minimum resources, such an algorithm is employed.
Let us look at an example. Say person A is a reseller who has a bag that can carry a maximum weight of 20 pounds. Person A has been tasked with going to a warehouse and filling the bag to capacity in such a way as to maximize the profit upon selling those items. What items should A pick at the warehouse in order to maximize the eventual revenue/ profit? Here A would follow a series of steps (i.e., an algorithm) before arriving at a decision. Person A would likely do the following:
- Look for the most expensive items that may also give him/ her a high markup
- Check their size, volume and weight to evaluate how many such items can be accommodated in the bag.
- Next look for the most in-demand items
- Check their size, volume and weight to evaluate how many such items can be accommodated in the bag.
- Consider all of the above then pick out the items.
In other words, person A would use the greedy algorithm here to get optimal solutions/ results. Here the optimal result would be picking out items that are not too big or heavy so as to be able to fit in the bag and at the same time, are fairly in demand and have a decent markup thus translating into higher revenues and profits.
Dynamic Programming algorithm
A dynamic programming algorithm works by remembering the results of a previous run and using them to arrive at new results. Such an algorithm solves complex problems by breaking it into multiple simple subproblems, solving them one by one and storing them for future reference and use.
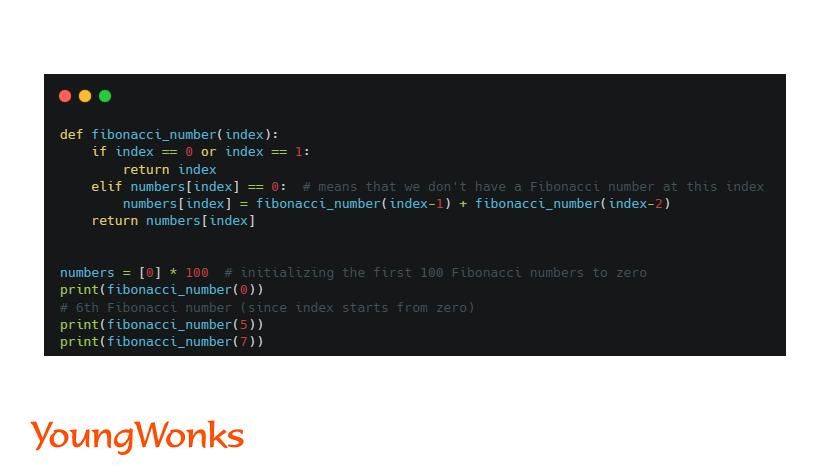
A common example here would be finding a number in the Fibonacci series. The Fibonacci series has numbers that are the sum of the previous two numbers. So, if one was asked to share the fifth number in the Fibonacci series, one would arrive at the number 5 since the series would start as 1, 1, 2, 3 and then 5. Now if one were asked to calculate the seventh number in the series, the algorithm would typically have one build on the work done so far and take it forward. So, in effect, one has remembered and used the results from the previous problem and deployed them to solve the current problem, thus arriving at the seventh number in the series, which is 13.
Divide and Conquer algorithm
Another effective method of solving many problems, here, as the name suggests, one divides the steps, aka the algorithm into two parts. In the first part, the problem is broken into smaller subproblems of the same type. The second part is where the smaller problems are solved and then their solutions are considered together (combined) to produce the final solution of the problem.
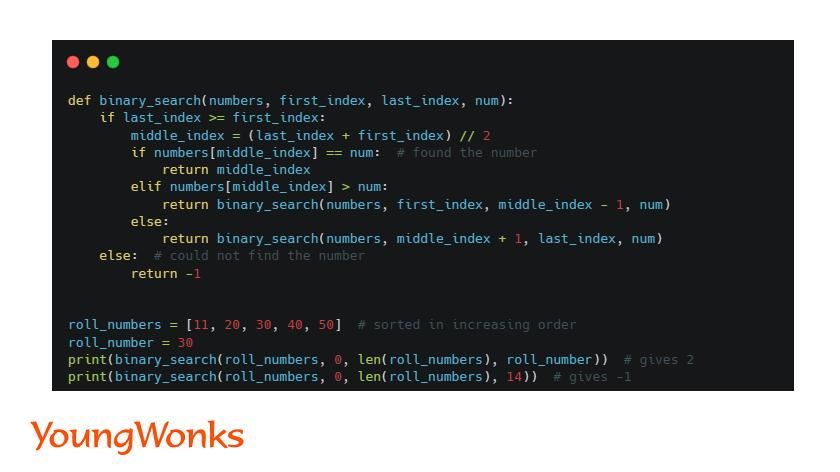
An example here would be a scenario where one has to find a student with a certain roll number - say 63 - in a school playground gathering. Now one way to do so would be to go about inquiring each child as to his/ her roll number. This, however, is not the quickest method.
A better way or algorithm would be one that goes like this:
- Have the students line up in ascending or descending order of their respective roll numbers.
- Split them into smaller groups - say of 50 students each - according to their roll numbers.
- Find the student group with roll numbers 51 to 100.
- Since 63 is less than the halfway (75) mark in this mark, go about inquiring in the first half of the group.
- Continue to enquire till you reach student with roll number 63.
Recursive algorithm
Recursive algorithm is one which involves repetition of steps till the problem is solved.
For instance, if one has to arrive at the greatest common factor (GCF) between any two numbers. Let's start with 14 and 18.
The algorithm here would be:
- Divide 18 by 14.
- Check the remainder (4).
- Divide 14 by 4.
- Check the remainder (2).
- Divide 4 by 2.
- Check the remainder (0).
- Since the 0 remainder was arrived at upon division by the number 2, the GCF here would be 2.
Similarly, if one had to find the GCF between 12 and 16, one would go through similar steps but with the new inputs so as to arrive at the new result.
So the algorithm here would be:
- Divide 16 by 12.
- Check the remainder (4).
- Divide 12 by 4.
- Check remainder (0).
- Since the 0 remainder was arrived at upon division by the number 2, the GCF here would be 4.
As shown above, the process remains the same and is thus repeated, which makes this a recursive algorithm.
Brute Force algorithm
A brute force algorithm involves blind iteration of all possible solutions to arrive at one or more solutions. A simple example of a brute force algorithm would be trying to open a safe. Without any knowledge of the combination that can open the safe, the only way forward would be trying all possible combinations of numbers to open it. The same would be the case for someone trying to get access to another person's email account. Trial and error would be the method employed here; in other words, the solution lies in applying brute force, and hence the name of the algorithm.
Backtracking algorithm
Backtracking algorithm is one that entails finding a solution in an incremental manner. There is often recursion/ repetition involved and attempts are made to solve the problem one part at a time. At any point, if one is unsuccessful at moving forward, one backtracks aka comes back to start over and find another way of reaching the solution. So backtracking algorithm solves a subproblem and if and when it fails to solve the problem, the last step is undone, and one starts looking for the solution again from the previous point.
An example would be when one plays chess. Typically, a good chess player contemplates the possible next move by the opponent in response to a certain move made by him/ her. Here each player is working out scenarios and often backtracking so as to arrive at the best possible way forward.
Algorithms in Python code
Problem: Figure out if a given number is odd or even

Problem: Figure out if a given number is prime or not
Problem: Finding a particular Fibonacci number
Problem: Using binary search to look for a kid with a certain roll number in a big school gathering
Problem: Finding the GCF/ HCF of two numbers

Problem: Using hit and try method to crack a password

Expanding Your Child's Coding Knowledge
To deepen your child's understanding of algorithms and their applications in various programming languages, consider enrolling them in specialized Coding Classes for Kids. These classes not only provide a strong foundation in algorithmic thinking but also introduce students to different programming environments. For those particularly interested in Python, one of the most versatile and beginner-friendly programming languages, Python Coding Classes for Kids can be an excellent starting point. Additionally, for children fascinated by the intersection of hardware and software, Raspberry Pi, Arduino, and Game Development Coding Classes offer hands-on experience in building and programming their own gadgets and games, further solidifying their understanding of algorithms in real-world applications.
*Contributors: Written by Vidya Prabhu with inputs by Rohit Budania; Lead image by: Leonel Cruz