Feb 19, 2024 By Team YoungWonks *
Understanding Search Algorithms
Before we delve into the specifics of Linear Search and Binary Search, let's establish a foundational understanding of search algorithms.
Search Algorithm
A search algorithm is a methodical approach to locate a particular item within a dataset. These algorithms play a crucial role in various domains, including data science, machine learning, and software engineering.
What is Linear Search?
Linear search, also known as sequential search, is a straightforward algorithm that sequentially traverses a sorted list until it finds the desired element. It's commonly employed when dealing with small datasets or linked lists, offering a simple and intuitive solution for locating the first element, whether it's a number, string, or any other data type. In a scenario where the dataset is sorted, linear search efficiently navigates through the sorted order, examining each element until it finds a match. Despite its simplicity, linear search serves as a foundational concept in programming tutorials and is often encountered in data structures courses and interview questions.
What is Binary Search?
Binary search represents a more sophisticated approach, particularly suitable for large datasets or arrays sorted in ascending or descending order. By repeatedly dividing the search space in half, binary search quickly homes in on the target element, making it highly efficient for locating integers, strings, or any other data types within a sorted list. Its average case time complexity of O(log n) ensures fast search operations, especially when dealing with datasets containing integers or half of the list. Binary search's efficiency is further highlighted in its applications, ranging from sorting algorithms to data science and machine learning tasks, making it a crucial tool for programmers and data scientists alike.
Both linear search and binary search offer valuable insights into the fundamentals of search algorithms and their practical applications in various programming languages and data structures. Whether you're visualizing the search process, implementing sorting algorithms, or tackling interview questions on data structures and algorithms (DSA), understanding the intricacies of linear and binary search is essential for navigating the vast landscape of computer science and programming languages.
How Linear Search Works?
Linear search, often referred to as sequential search, is one of the simplest search algorithms. It sequentially traverses each element of the dataset until it finds the desired element.
The linear search algorithm iterates through each element of the array until it finds the target element. If the element is present, it returns its index; otherwise, it returns -1.
Python Implementation of Linear Search

Function Definition: This defines a function named linear_search that takes two parameters: arr (the array to be searched) and target (the element to be searched for).
Linear Search Algorithm: It iterates through each element of the array using a for loop and checks if the current element is equal to the target. If a match is found, it returns the index of the element (return i); otherwise, it returns -1 to indicate that the target is not found.
Java Implementation of Linear Search

Method Definition: This defines a static method named linearSearch in the class SearchAlgorithms that takes two parameters: arr (the array to be searched) and target (the element to be searched for).
Linear Search Algorithm: It iterates through each element of the array using a for loop and checks if the current element is equal to the target. If a match is found, it returns the index of the element; otherwise, it returns -1 to indicate that the target is not found.
JavaScript Implementation of Linear Search

Function Definition: This defines a function named linearSearch that takes two parameters: arr (the array to be searched) and target (the element to be searched for).
Linear Search Algorithm: It iterates through each element of the array using a for loop and checks if the current element is equal to the target. If a match is found, it returns the index of the element; otherwise, it returns -1 to indicate that the target is not found.
Time Complexity of Linear Search
O(n) - Linear search has a time complexity proportional to the number of elements in the dataset.
Space Complexity of Linear Search
O(1) - Linear search requires constant space as it doesn't utilize additional data structures.
Applications and Prerequisites of Linear Search
- Linear search is suitable for small datasets or unsorted arrays.
- It serves as a foundational concept for beginners in programming and data structures.
How Binary Search Works?
Binary search is a more efficient search algorithm, particularly effective for large datasets or sorted arrays. It follows a divide and conquer strategy, repeatedly dividing the search space in half until the target element is found.
Binary search requires the dataset to be sorted. It compares the target value with the middle element of the array. If the target matches the middle element, the search is complete. Otherwise, it narrows down the search space by half based on the comparison result.
Python Implementation of Binary Search

Function Definition: This defines a function named binary_search that takes two parameters: arr (the sorted array to be searched) and target (the element to be searched for).
Binary Search Algorithm: It initializes two pointers, low and high, representing the start and end indices of the array respectively. It repeatedly narrows down the search space by adjusting these pointers until the target is found or the search space is exhausted.
Loop: Inside the while loop, it calculates the mid index as the average of low and high. It then compares the element at the mid index with the target:
- If the target matches the middle element, it returns the index.
- If the target is greater than the middle element, it updates low to mid + 1 to search in the right half.
- If the target is less than the middle element, it updates high to mid - 1 to search in the left half.
Return Value: If the target is not found after the loop completes, it returns -1.
Java Implementation of Binary Search

Method Definition: This defines a static method named binarySearch in the class Search Algorithms that takes two parameters: arr (the sorted array to be searched) and target (the element to be searched for).
Binary Search Algorithm: It initializes two pointers, low and high, representing the start and end indices of the array respectively. It repeatedly narrows down the search space by adjusting these pointers until the target is found or the search space is exhausted.
Loop: Inside the while loop, it calculates the mid index as the average of low and high. It then compares the element at the mid index with the target:
- If the target matches the middle element, it returns the index.
- If the target is greater than the middle element, it updates low to mid + 1 to search in the right half.
- If the target is less than the middle element, it updates high to mid - 1 to search in the left half.
Return Value: If the target is not found after the loop completes, it returns -1.
JavaScript Implementation of Binary Search
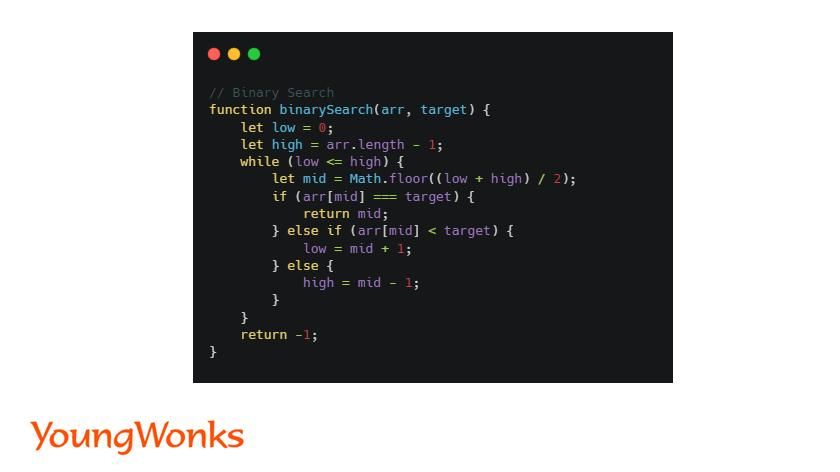
Function Definition: This defines a function named binary Search that takes two parameters: arr (the sorted array to be searched) and target (the element to be searched for).
Binary Search Algorithm: It initializes two pointers, low and high, representing the start and end indices of the array respectively. It repeatedly narrows down the search space by adjusting these pointers until the target is found or the search space is exhausted.
Loop: Inside the while loop, it calculates the mid index as the average of low and high. It then compares the element at the mid index with the target:
- If the target matches the middle element, it returns the index.
- If the target is greater than the middle element, it updates low to mid + 1 to search in the right half.
- If the target is less than the middle element, it updates high to mid - 1 to search in the left half.
Return Value: If the target is not found after the loop completes, it returns -1.
Time Complexity of Binary Search
O(log n) - Binary search exhibits logarithmic time complexity, making it highly efficient for large datasets.
Space Complexity of Binary Search
O(1) - Binary search has constant space complexity as it doesn't require additional memory allocations.
Applications and Prerequisites of Binary Search
- Binary search is optimal for large datasets or sorted arrays.
- Understanding of basic programming concepts and sorting algorithms is essential for implementing binary search.
Linear Search vs Binary Search: A Comparative Analysis
Now, let's compare Linear Search and Binary Search across various dimensions:
Efficiency
Linear Search: Efficient for small datasets but becomes increasingly slower as the dataset size grows.
Binary Search: Highly efficient, especially for large datasets, due to its logarithmic time complexity.
Time Complexity
Linear Search: O(n) - Linear time complexity.
Binary Search: O(log n) - Logarithmic time complexity.
Space Complexity
Both Linear Search and Binary Search have a space complexity of O(1), indicating constant space requirements.
Dataset Requirement
Linear Search: Works with both sorted and unsorted arrays.
Binary Search: Requires the dataset to be sorted for optimal performance.
Number of Comparisons
Linear Search: Worst-case scenario requires n comparisons.
Binary Search: In each step, the search space is halved, leading to fewer comparisons. Worst-case scenario requires log n comparisons.
Practical Applications
Linear Search: Suitable for small datasets or when simplicity is preferred over efficiency.
Binary Search: Widely used in scenarios requiring efficient search in large datasets or sorted arrays.
Other Variants and Considerations
While Linear Search and Binary Search are fundamental, there are other variants and considerations worth exploring:
Interpolation Search: Particularly efficient for uniformly distributed datasets.
Half-Interval Search: Used to find roots of continuous functions within given intervals.
Binary Trees
Binary trees are not directly related to linear search, as linear search typically operates on linear data structures like arrays or linked lists. However, in binary search, binary trees play a crucial role as they provide a structured representation of sorted data, facilitating the efficient divide-and-conquer approach employed by the binary search algorithm.
Iteration
In both linear and binary search algorithms, iteration plays a pivotal role in traversing the dataset and determining the location of the target element. In linear search, iteration entails sequentially examining each element of the array until a match is found or the end of the dataset is reached. This iterative process ensures thorough coverage of the dataset, albeit with a linear time complexity, making it suitable for smaller datasets or unsorted arrays. Conversely, in binary search, iteration follows a more refined approach, where the search space is systematically halved with each iteration. This iterative refinement significantly reduces the search time, leading to a logarithmic time complexity, ideal for large datasets or sorted arrays. In both cases, iteration serves as the driving force behind the search process, enabling the algorithms to efficiently navigate through the dataset and locate the target element.
Best Case Scenario
The best case scenario for linear search occurs when the target element is found at the very beginning of the dataset. In this case, the algorithm only needs to perform a single comparison, resulting in a time complexity of O(1). However, it's important to note that this scenario is rare, and the average and worst-case time complexities of linear search remain O(n).
On the other hand, the best case scenario for binary search occurs when the target element is located exactly at the middle of the dataset. In this scenario, the algorithm can immediately determine the target's position with just one comparison, resulting in a time complexity of O(1). However, binary search's dataset must be sorted for this scenario to be applicable. Additionally, binary search's average and worst-case time complexities are O(log n), making it significantly more efficient than linear search for large datasets.
Visualization
Visualization plays a crucial role in understanding and analyzing algorithms like linear search and binary search. By visualizing the search process, programmers can gain deeper insights into how these algorithms work and identify potential optimizations or pitfalls. Let's explore how visualization can enhance our understanding of both linear search and binary search:
Linear Search Visualization
In linear search, the algorithm sequentially scans each element in the dataset until it finds the target element or reaches the end of the list. Visualizing this process can be done by representing the dataset as a linear array or a linked list. As the algorithm progresses, each element can be highlighted or marked to indicate whether it's been compared to the target element. This visualization helps users understand the linear nature of the search process and how the algorithm iterates through each element until a match is found or the end of the list is reached.
Binary Search Visualization
Binary search, on the other hand, follows a divide and conquer approach by repeatedly dividing the search space in half. Visualizing binary search involves representing the sorted dataset as a binary tree, where each node represents an element in the dataset. As the algorithm progresses, users can see how the search space is halved in each iteration, with the target element being compared to the middle element of the current subarray. This visualization provides insights into the efficiency of binary search and how it quickly converges on the target element by reducing the search space exponentially.
Conclusion
In conclusion, Linear Search and Binary Search are two fundamental search algorithms with distinct characteristics and applications. Linear search, though simple, is suitable for small datasets or when the elements are unsorted. It efficiently navigates linear data structures like arrays or linked lists and can be visualized as sequentially examining each element until a match is found, potentially reaching the last element. On the other hand, Binary search, leveraging its divide and conquer strategy, excels in efficiency, making it optimal for large datasets or sorted arrays. It efficiently searches through half of the list in each iteration, resulting in a logarithmic time complexity. Additionally, binary search can be visualized as recursively dividing the search space until the target element is located. Understanding the nuances of these algorithms is crucial for programmers and computer science enthusiasts alike. Whether you're a beginner exploring the basics of search algorithms or an experienced developer optimizing performance, mastering Linear and Binary Search opens doors to a deeper understanding of algorithmic principles and problem-solving techniques.
Coding Education for Aspiring Programmers
In understanding the intricacies of algorithms like linear and binary search, learners can significantly boost their problem-solving skills, a vital component of programming. For youngsters eager to dive deeper into the world of coding, Coding Classes for Kids at YoungWonks offer a well-rounded curriculum tailored for various age groups. Particularly, those with a keen interest in one of the most popular programming languages can take advantage of Python Coding Classes for Kids. Meanwhile, hands-on enthusiasts can explore hardware programming with Raspberry Pi, Arduino and Game Development Coding Classes, perfect for budding hardware engineers and game developers.
*Contributors: Written by Disha N; Edited by Rohit Budania; Lead image by Shivendra Singh

